Edge Plasma and Divertor Detachment
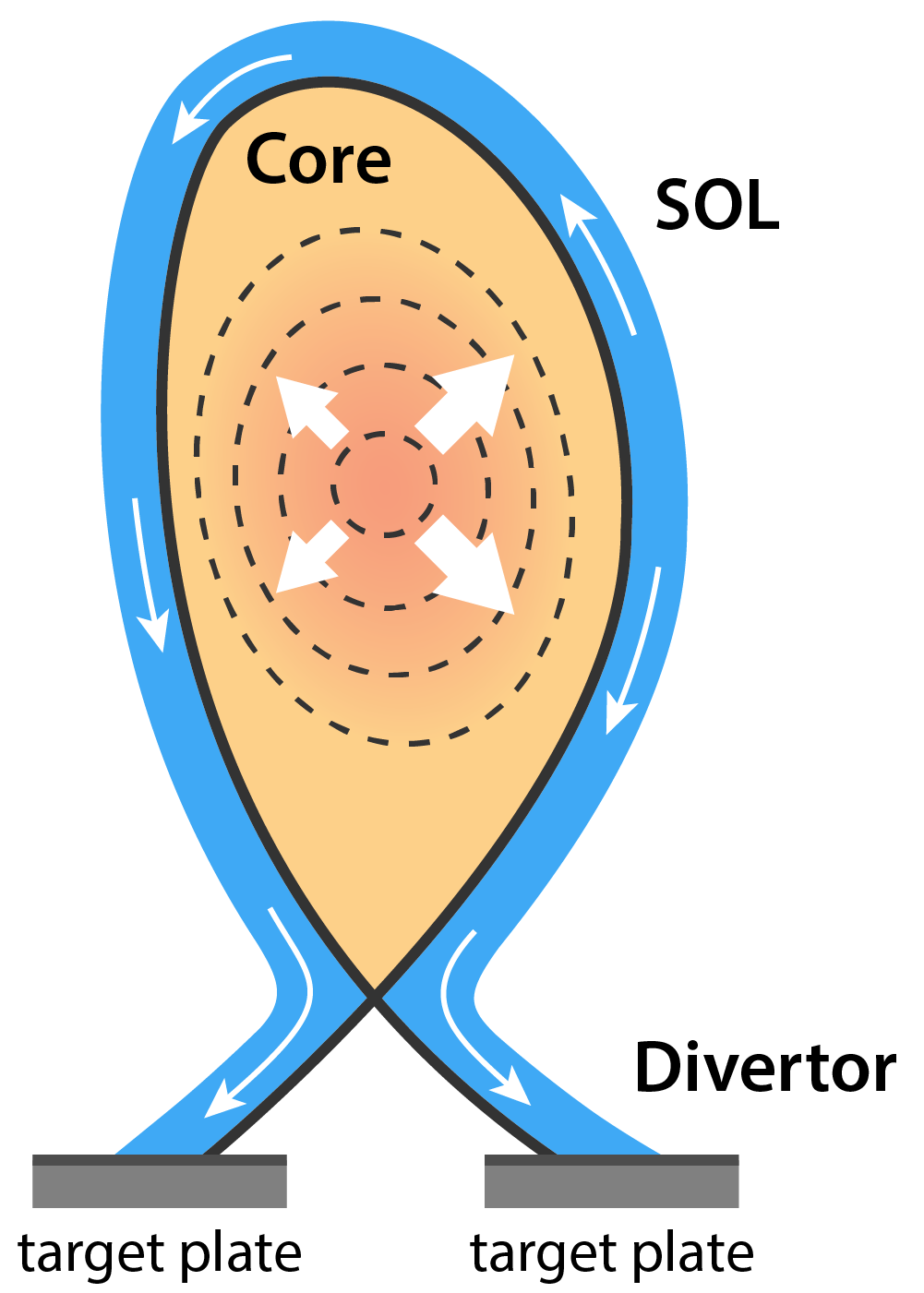
flows towards the divertor target plates.
We use coupled plasma fluid and kinetic neutral particle codes (like SOLPS-ITER) to study the physics of the plasma - neutral gas interaction in tokamak divertors. The same plasma - neutral gas conditions are recreated in linear plasma generators. like MAGNUM-PSI, where they can be studied in greater detail. Given the complex physics and multi-dimensional character of these systems, these codes typically run on supercomputers taking many hours to obtain a single steady state solution. As a result, dynamic simulations with these codes are almost prohibitively computationally demanding. For the purpose of dynamic simulations we have developed a reduced 1 dimensional model (DIV1D).
Electron Cyclotron Resonance Heating and Current Drive
We contribute numerical codes for the modelling of electron cyclotron resonance heating and current drive to the EUROfusion Integrated Tokamak Modelling platform. We have co-developed the TORAY-FOM ray-tracing code for the description of EC wave propagation and absorption. Rays can be traced using either the cold or warm plasma dispersion relation. Options are provided for weakly or fully relativistic calculations of the dielectric tensor. In addition the current drive efficiency can be calculated using the adjoint technique. We have developed the bounce-averaged quasi-linear Fokker-Planck code RELAX, which allows to calculate the modified electron distribution function and current drive under conditions of high power ECRH and ECCD. We have provided both codes with options to model ECRH and ECCD in the presence of magnetic islands as created by tearing modes.
Neoclassical Tearing Modes and their control
We model the evolution of neoclassical tearing modes (NTMs) using models of increasing levels of accuracy and complexity. A zero dimensional description is provided by the generalized Rutherford equation which provides the evolution of the width of the magnetic island. We study the models for the most relevant contributions in the Rutherford equation including the classical stability, the neoclassical drive, and the stabilizing terms from local heating and current drive. In the next step of complexity, we have developed a 2D reduced MHD code. With this code we have provided the validation of the neoclassical and current drive terms in the generalized Rutherford equation (see Highlights).